
Published in: IGARSS 2024 - 2024 IEEE International Geoscience and Remote Sensing Symposium
Date of Conference: 07–12 July 2024
Date Added to IEEE Xplore: 05 September 2024
DOI: 10.1109/IGARSS53475.2024.10640387
This study delves into the realm of satellite image super-resolution, not only focusing on increasing resolution but also overcoming unique distortions. It addresses the challenges posed by the absence of training data...
Key words— Satellite data, machine learning, image enhancing, image deblurring, super-resolution
Satellite imaging serves as an invaluable tool for comprehensive Earth observation, enabling us to monitor and analyze diverse landscapes with unprecedented detail. Despite the strides made in satellite technology, the quest for higher precision persists, driving the need for innovative approaches in image enhancement.
In the pursuit of refining satellite imagery, two critical challenges demand attention: image distorsions and the imperative to ensure consistency in essential agro- indices. This study embarks on a journey to address these challenges comprehensively, introducing advanced techniques that not only mitigate the effects of image distorsions but also guarantee the stability of crucial agro- indices, such as the NDVI (Normalized Difference Vegetation Index).
Atmospheric blur, defocusing, and noise can have different parameters. The task of image enhancement is to determine these parameters and solve the inverse function of these distortions. This will allow us to reproduce a clear image. The inverse distortion function is represented in (1):
where Φ is the image distortion function,
θη is a parameter vector,
Is is the latent sharp version of the distorted image Id.
\[ I_s = \Phi^{-1}\left( I_d ; \theta_\eta \right) (1) \]
In real-world scenarios, the distortion model Φ −1 is unknown, necessitating its determination. The distortion function can be very complex to calculate and even more challenging to solve for the inverse problem.
Neural networks contribute to solving the task of approximating functions that are challenging or even impossible to define analytically. They learn from extensive datasets, aiming to make predictions or replicate input- output relationships optimally. However, the challenge arises when dealing with satellite imagery, as we lack the capability to generate thousands of images from our desired satellite, followed by creating thousands of identical images free from noise, blur, and other distortions for training the neural network.
In our approach, we aim to shift away from the endeavor of seeking the parameters and solution of the distortion function. Instead, our focus lies on emulating the distortion function. This method facilitates the generation of an unlimited amount of synthetically distorted data, matching distortion parameters, while preserving clear originals without any distortion. This capability enables the training of a neural network for image enhancement using a batch of both high-quality and distorted images as inputs.
In this section, we will describe our approach to make image enhancement:
Stage 1: We train a distortion network, referred to as the "Distortion Network". For training we use one snapshot from our satellite and one high-quality template fromanother source. The network is trained to approximate the high-resolution and quality features of the template onto our lower quality satellite image.
Stage 2: In the next, we utilize the Distortion Network to generate training data by inputting a high-quality image dataset. The network then produces a diverse set of data with distortions analogous to those introduced by our distortion function.
Stage 3: In the third phase, we leverage both high-quality and low-quality datasets obtained through the Distortion Network. These datasets serve as inputs for training the Super-Resolution Generative Adversarial Network (SRGAN)[1]. By utilizing this approach, we train SRGAN to enhance our images, allowing the model to learn and generate high-resolution representations from low-resolution inputs distorted in accordance with our specific distortion function. The outcome is a model capable of improving the quality of our satellite snapshots, addressing distortions and enhancing details.
Stage 4: The final stage focuses on post-processing the output image, addressing potential nonlinear changes introduced by the neural network. The primary method involves comparing images both before and after neural network processing, followed by incorporating the difference into the enhanced image to counteract nonlinearity. This ensures the uniformity of average values across channels, NDVI, and similar characteristics.
For most cases of super-resolution testing in satellite imagery, as in [2], the evaluation of results is conducted by comparing them with high-resolution images used to train the neural network. In our case, as in many real-world scenarios, there are no available high-resolution images corresponding to the same time and location. Therefore, we will conduct testing in two stages. Firstly, we will visually compare and verify the characteristics on real images, and secondly, we will create synthetically distorted data and their super-resolution images for evaluating results using PSNR metrics and SSIM.
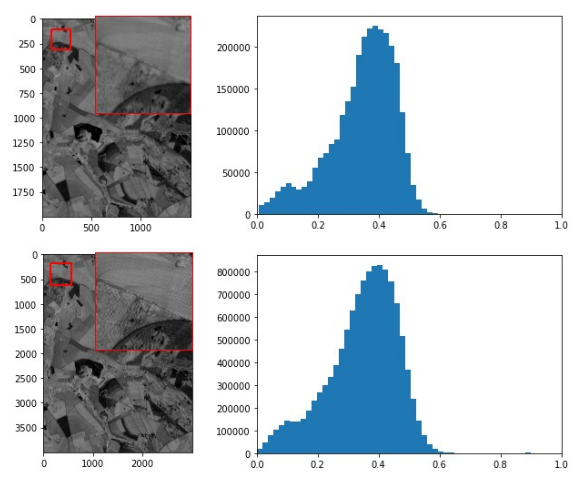
For the first part we conducted all experiments using real data from the EOS SAT-1 satellite. EOS SAT-1 is an optical satellite equipped with 11 agri-related bands that provide valuable insights to farmers and other industry stakeholders. We conducted experiments both on a per- channel basis and across multiple channels. An example of input and improved image will be presented in Figure 1.

Example of visual comparision of proposed approach in Figure 2 shows that other single image super- resolution methods are not very effective for images like EOS SAT-1. However, our approach allows for significant enhancement in image quality.

In Table 1, we provide data for the image before and after enhancement, using the example of the panchromatic channel. The Laplacian variance metric shows increased sharpness, while the mean value metric indicates no negative nonlinear changes to the image.
| Before | After | |
|---|---|---|
| Size | 400 × 300 | 800 × 600 |
| Resolution | 1.5m | 0.75m |
| Mean | 26.6 | 26.6 |
| Laplacian variance [4] | 2.1 (8-bit size 400×300) |
43.4 (8-bit size 400×300) |
We conducted numerical experiments using EOS SAT data to compare the NDVI values before and after enhancement. To construct the NDVI, we used the RED and NIR channels. SRGAN enhancement and post-processing were applied to each channel, followed by the calculation of a higher-resolution NDVI based on them. The NDVI images are presented in Figure 3.
| PSNR | SSIM | |
|---|---|---|
| EDSR [7] | 26.38 | 0.72 |
| SRGAN [1] | 26.33 | 0.71 |
| OUR | 31.66 | 0.94 |
Analyzing our work and similar publications [9] [10], we can assert that our approach has advantages over popular state-of-the-art methods [1][7]. Using a distortion model, as in our work and [9], results in better image reconstruction compared to conventional super-resolution pipelines. Our training method differs from [9] in that they use a random variation within the range of 0.2–0.8. In contrast, we found this random blur approach to be ineffective since the randomly selected distortions did not match our real model. Consequently, our approach better selects the appropriate distortion for training, as it replicates the real model. One drawback of this method is its validity only for the specific satellite for which the model is designed.
Using neural networks for image processing significantly enhances image quality and resolution. However, unlike precise mathematical formulas, neural networks' weights and performance depend on factors like training time and dataset size [5][6]. Thus, despite improvements in resolution and reduced blurring, the mean value, standard deviation, and color histogram may change. Most super-resolution pipelines involve normalization, neural network inference, and denormalization. These processes are standardized and widely documented, ensuring consistent mean and standard deviation coefficients at both input and output, even if the output visually differs.
The neural network's weights, influenced by training time, architecture, and dataset, mean that statistical characteristics like mean, standard deviation, or per-pixel difference can vary from the original. Unlike mathematical methods such as cubic interpolation, standard normalization and denormalization usually lack feedback for verifying these characteristics post-super-resolution.
In many approaches, this is addressed by better network architecture, changing loss functions, and other methods [12]. In publication [10], histogram normalization was used on the already trained network to achieve better quality. We used a similar approach, shown in Figure 4, which allows us to avoid the aforementioned drawbacks.
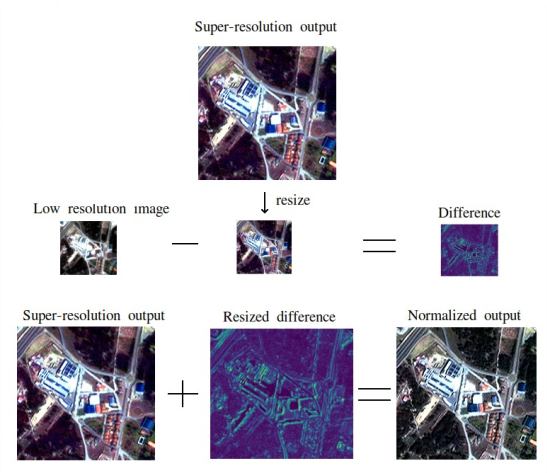
In conclusion, our multi-stage approach to image enhancement integrates the training of a Distortion Network and the utilization of a Super-Resolution Generative Adversarial Network (SRGAN). By training the Distortion Network to emulate distortion functions and generating diverse training data, we empower SRGAN to enhance satellite images, effectively addressing specific distortions. The post-processing stage ensures consistency and mitigates nonlinear changes introduced by the neural network, maintaining uniformity in average values across channels and key characteristics. This comprehensive methodology contributes to the advancement of image enhancement for satellite-based agricultural monitoring.